This page covers an introduction to the Barnes-Hut tree, with sample Javascript source code.

Introduction to the problem of gravity simulations
Javascript + provessing.js on KhanAcademy primer
The Barnes-Hut solution
Including other forces
Example implementations

Introduction to the problem of gravity simulations

The most straightforward numerical algorithm for a gravitational n-body simulation is as follows:

Start with your list of positions $\vec{x}_i$, velocities $\vec{v}_i$, and masses $m_i$,
Calculate your acceleration vectors, $\vec{a}_i=\sum _{j\neq i} G m _ j \frac{\vec{x} _ j-\vec{x} _ i}{\|\vec{x} _ j-\vec{x} _ i\|^3}$
Numerically integrate. Say, send $\vec{x}_i:=\vec{x } _ i+\vec{v} _ i \Delta t$ (for all $i$), and send $\vec{v} _i:=\vec{v} _ i+ \vec{a}_i\Delta t$.

The sum in the second step is where the problem is. If you do the most straightforward implementation with $N$ particles, you calculate $N(N-1)$ distances per time step. If you do things a bit fancier, you can make sure you only calculate each distance once and reduce it to $\frac{1}{2}N(N-1)$ distance calculations per frame. But this is still $N^2$ growth. It works well enough for 100 particles, but if you’re trying to simulate a million particles, that’s $10^{12}$ distance calculations per frame, which is truly terrible.

Obviously we can improve on this! If we want to find the gravitational acceleration on us due to Andromeda, we don’t need the distances to every particle in Andromeda individually, we only need the mass of Andromeda and the distance to the center of mass of Andromeda. I.e., instead of the following diagram, where we have $12$ particles and $11$ distance calculations per particle ($=132$ distances per frame)…

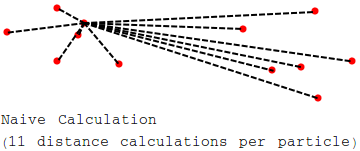
brute force n squared algorithm

we could do the following, with $12$ particles but only $6$ distance calculations per particle ($=72$ distances per frame):

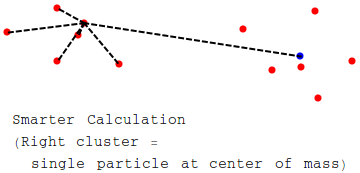
Smarter way to calculate distances by using a center of mass approximation

Wouldn’t it be nice if we had an algorithm to choose how to cluster particles and replace them with their center of mass when needed, so that we can just find the distance to the center of masses?

The Barnes-Hut tree algorithm does exactly this. The following is a demonstration of the Barnes-Hut algorithm. Place your mouse cursor inside the javascript canvas, and watch as the algorithm miraculously decides where to approximate black particles (the true distribution), with the red particles (the center of mass of some subset of black particles). You can view the source code on KhanAcademy or below.

The Barnes-Hut tree algorithm is very flexible. It has three steps:

Build a quadtree. This is the efficient data structure that makes everything possible.
For each particle, traverse the quadtree to a sufficient depth. This gives you the center of masses to which you need to calculate distances, and so this step gives you the acceleration on each particle.
Numerically integrate using your algorithm of choice. (Velocity Verlet, Euler, whatever.)

Note, I use the word “quadtree” because all the examples I give here are in two dimensions. In one dimension it would be a bintree, in three dimensions an octree, in four dimensions a hexidecitree (I guess), et cetera. In fact, the link near the bottom of this page, part-nd, is an arbitrary dimension tree code.

0 Javascript + processing.js on KhanAcademy primer

For the uninitiated, here’s some weird stuff about Javascript.

0.1 Loose Typing.

Javascript is loosely typed. Variables are declared with “var x=0;”. A “var” can be a function, integer, double, “undefined”, what have you. The following is valid:

var x='abcd';
x=undefined;
x=0.6;
x=function(y){return y*y;};

You might ask, “but David, if x(2) return 4 after the last line, what happens if I call x(“Hello”)?” To which I would respond, “exactly!”

0.2 The processing.js library.

Processing.js has a lot of available functions and it makes drawing to an html5 canvas easy. Since Java applets are dead, this is my go to choice, and it’s implemented on Khan Academy computer science with a nice IDE so that you don’t have to do anything fancy to start using it.

0.3 Object declaration

Object declaration in Javascript is a bit weird. This code is actually inefficient, and you can do stuff with what are called object prototypes to speed up your program, but that’s not too important here. The following method works to create a particle with member variables and instantiate them.

var particle=function(x,y){
    this.x=x;
    this.y=y;
    this.toText=function(){
        println("("+this.x+","+this.y+")"); //A processing.js function
    };
    this.draw= function() {
        ellipse(x,y,3,3); //A processing.js function that draws to the canvas
    };
};
var p=new particle(200,300);
p.toText(); //access a member function and print "(200,300)"
p.x=240; //change a member variable
p.toText=function(){}; //change a member function

1 The Barnes-Hut solution

So, in order to avoid repeating all the online resources about tree data structures, I’ll focus on the 2D javascript object-oriented implementation and hopefully a better understanding of the tree structure comes to you when you pore over the code!

I’ll give two javascript programs. The first one uses a recursive function and a recursive data structure to create the quadtree. the second one includes all the code of the first, but also handles the details involving the mass and center of mass, as well as traversing the quadtree.

1.1 Building a quadtree

This section covers the details of writing the following applet. The code is based on processing.js so that it can run on KhanAcademy. Click here to view the source code of the applet on KhanAcademy.

Click to add a new particle to the quadtree:

First I define a particle object for us to instantiate, with some useful functions:

var particle=function(x,y){
    this.x=x;
    this.y=y;
    this.toText=function(){
        println("("+this.x+","+this.y+")"); //A processing.js function
    };
    this.draw= function() {
        ellipse(x,y,3,3); //A processing.js function that draws to the canvas
    };
};

We’re in two dimensions, so each node (or “cell”) can have four subnodes. For a given node, we have three possible states. Keep an eye out because these states will be used later:

State 1. It’s empty. It doesn’t point to any subnodes nor a particle.
State 2. It has subnodes. It points to four subnodes and does not point to a particle.
State 3. It has a particle. It points to a particle and doesn’t point to any subnodes.

We need to label the four subnodes. I usually get confused if I use the notions of “left”, “right”, “up”, and “down” in my code because of all the issues of right-handedness or left-handedness and which direction is vertical, et cetera. So instead of labeling the four subnodes “top left” and “bottom right”, I label the nodes depending on whether their x/y coordinate is smaller or larger numerically. So in my code I denote variables corresponding to lower bounds or lower nodes by “s” for small and variables corresponding to upper bounds/higher nodes by “l” for large. (This sounds stupid until you’re forever confused by a naming convention that leaves “up” to mean traveling down on your monitor!).

var quadtreeNode=function(smallx,smally,largex,largey){
    //variables described as "vars" are only accessible from local functions

    //the four bounds on the quadtree node rectangle
    var xs=smallx;
    var xl=largex;
    var ys=smally;
    var yl=largey;

    //the center, for later usage
    var cx=(smallx+largex)/2;
    var cy=(smally+largey)/2;

    //variables described as "this." are accessible from the outside
    //saying something equals undefined doesn't do any useful instantiation
    //AFAIK, but it's for readability.

    //middle s is whether the x value is small or large
    //rightmost s is whether the y value is small or large.
    this.nss=undefined; //small quadrant
    this.nsl=undefined;
    this.nls=undefined;
    this.nll=undefined;

    //variable for storing 
    this.p=undefined;

    //[...]
};

//We can instantiate the object as follows
var tree=new quadtreeNode(0,0,400,400);

To illustrate the power of the recursive object oriented data structure, let’s suppose that the tree is filled up in the way described. It is in one of the three states described above. If it’s empty, we do nothing and return. If it’s full of a particle, we draw the particle. If it’s full of subnodes, we draw a subnodes and a little “crosshair” shape to partition the subnodes into four sections:

var quadtreeNode=function(smallx,smally,largex,largey){

    //[...]

    this.draw= function() {
        if(this.p!==undefined){ //State 3
            this.p.draw();
        }
        if(this.nss!==undefined){ //State 2
            //draw a "crosshair" running through the center of the node
            line(xs,cy,xl,cy);
            line(cx,ys,cx,yl);
            
            //Draw all the child nodes and the particles they contain.
            this.nss.draw();
            this.nsl.draw();
            this.nls.draw();
            this.nll.draw();
        }
    };
};

So we have the ability to store a clever data structure, we have the ability to draw the clever data structure, but we can’t yet create it, and of course that takes the most effort. The idea is to make a single function called “addParticle”. We’ll have a parent quadtree node, and we’ll just call “addParticle” some large number of times on it until we’ve added all the particles we want. The function “addParticle” will do the appropriate thing. Recall that states 1, 2, and 3, are whether the node is empty, has four subnodes, or has a particle, respectively.

If a given node is in state 1, calling “addParticle” will just make the node point to a particle. (so it sends the node into state 3).

If a given node is in state 3, we can’t add another particle, so we have to create four subnoes (sending the node to state 2) and pass the particle down to the correct subnode.

If a given node is in state 2, all we have to do is pass the particle down to the correct subnode. The node stays in state 2.

var quadtreeNode=function(smallx,smally,largex,largey){

    //[...]

    this.addParticle=function(p){
        if(this.nss===undefined){
            if(this.p===undefined){
                //We're in state 1, and we send the node to state 3.
                this.p=p;
                return;
            } else { 
                //We're in state 3.
                //a failsafe: If the particles are on top of each other we'll recurse infinitely! 
                //I solve the problem by just excluding the particle.
                var tmp=this.p;
                if(abs(tmp.x-p.x)<0.001 && abs(tmp.y-p.y)<0.001){
                    return;
                }
                //Send the particle to state 2. 
                this.nss=new quadtreeNode(xs,ys,cx,cy);
                this.nsl=new quadtreeNode(xs,cy,cx,yl);
                this.nls=new quadtreeNode(cx,ys,xl,cy);
                this.nll=new quadtreeNode(cx,cy,xl,yl);
                this.p=undefined;
                //clever recursion. Since we're in state 2 now we know exactly what this does.
                this.addParticle(tmp);
                this.addParticle(p);
            }
        } else { //We're in state 2.
            /*We want to call addParticle(p) on the correct subcell! 
            This can be done in a few different ways. For brevity I like
            a little binary trick. I make a number "c" whose bits
            correspond to what cell we're in. If the leading bit is 
            zero we're in one of the two smaller x cells. If the leading bit
            is one we're in one of the two larger x cells. The second bit 
            corresponds to the y larger/smaller value.*/
            var a=(p.x>=cx)?1:0;
            var b=(p.y>=cy)?1:0;
            var c=a|(b<<1);
            if(c===0){
                this.nss.addParticle(p);
            } else if(c===1){
                this.nls.addParticle(p);
            } else if(c===2){
                this.nsl.addParticle(p);
            } else if(c===3){
                this.nll.addParticle(p);
            }
            return; //we stay in state 2.
        }
    };
};

That’s it! The full code, which includes interactivity and adding a full list of particles, can be found on KhanAcademy at this link.

1.2 Traversing the quadtree

So far we’ve just done stuff that would be covered in a data structures class. The thing that separates the kids from the adults, or the computer scientist from the computational physicist, is what you do with the data structure.

Well first, let’s add a few things. Let’s define a gravitational constant, add a “mass” parameter to our particle, as well as x and y positions and accelerations to be filled.

var Gconstant=100;

var particle=function(x,y){
    this.x=x;
    this.y=y;
    this.m=1;
    this.accelx=0;
    this.accely=0;
    this.toText=function(){
        println("("+this.x+","+this.y+")");
    };
    this.draw= function() {
        ellipse(x,y,3,3);
    };
};

And also, for each cell, we want to keep track of the center of mass and the total mass of each cell. To do this, I add variables “cmxsum”, “cmysum”, and “msum”, representing $\mathrm{cmxsum}=\sum_i x_i m_i$, $\mathrm{cmysum}=\sum_i y_i m_i$, and $\mathrm{msum}=\sum_i m_i$, where the sum is taken over all particles in the node and all particles in every subnode of the current node. This can be handled by adding in a few choice lines to “addParticle”.

var quadtreeNode=function(smallx,smally,largex,largey){
    var xs=smallx;
    var xl=largex;
    var ys=smally;
    var yl=largey;
    var cx=(smallx+largex)/2;
    var cy=(smally+largey)/2;
//middle s is whether the x value is small or large
//rightmost s is whether the y value is small or large.
    this.nss=undefined; //small quadrant
    this.nsl=undefined;
    this.nls=undefined;
    this.nll=undefined;
    this.p=undefined;
    
    var cmxsum=0;
    var cmysum=0;
    var msum=0;
    
    this.addParticle=function(p){
        if(this.nss===undefined){
            if(this.p===undefined){

                cmxsum=p.x*p.m;
                cmysum=p.y*p.m;
                msum=p.m;

                this.p=p;
                return;
            } else {
                var tmp=this.p;
                if(abs(tmp.x-p.x)<0.001 && abs(tmp.y-p.y)<0.001){
                    return;
                }
                //Send the particle to state 2. 
                this.nss=new quadtreeNode(xs,ys,cx,cy);
                this.nsl=new quadtreeNode(xs,cy,cx,yl);
                this.nls=new quadtreeNode(cx,ys,xl,cy);
                this.nll=new quadtreeNode(cx,cy,xl,yl);
                this.p=undefined;

                cmxsum=0;
                cmysum=0;
                msum=0;

                this.p=undefined;
                this.addParticle(tmp);
                this.addParticle(p);
            }
        } else {
            var a=(p.x>=cx)?1:0;
            var b=(p.y>=cy)?1:0;
            var c=a|(b<<1);

            cmxsum+=p.x*p.m;
            cmysum+=p.y*p.m;
            msum+=p.m;

            if(c===0){
                this.nss.addParticle(p);
            } else if(c===1){
                this.nls.addParticle(p);
            } else if(c===2){
                this.nsl.addParticle(p);
            } else if(c===3){
                this.nll.addParticle(p);
            }
            return;
        }
    };

    //[...]
};

Now we can add the desired function to calculate the accelerations. The idea is simple: We have our top level quadtree node, and we call a function “calculateAccel(p)” on it. If the given node is empty, this function does nothing. If the given node has a particle in it, it calculates the force on the passed in particle p, due to the mass in the node, and stores it inside p. If the given node has subnodes, we can do one of two things. We can either call calculateAccel(p) on all four subnodes, or we can stop the recursion and calculate the force on p due to the center of mass equivalent of the node.

This decision is governed by a heuristic. The heuristic is this: take the distance between the particle and the cell center of mass, $d$. Define a quantity $s$ to be the “size” of the node, defined to be the average of its width and height. If the quantity $s/d$ is smaller than some value, don’t recurse, and instead just use the center of mass approximation.

In this program, I don’t actually calculate accelerations, I just draw the tree structure, so I call my function “drawHut” instead.

var quadtreeNode=function(smallx,smally,largex,largey){

    //[...]

    this.drawHut=function(p){
        if(isNaN(cmxsum)||isNaN(cmysum)||(msum<=0)){
            return;
        }
        var x=cmxsum/msum;
        var y=cmysum/msum;
        var s=((xl-xs)+(yl-ys))/2;
        var d=sqrt((x-p.x)*(x-p.x)+(y-p.y)*(y-p.y));
        if(s/d<0.5){ //don't recurse
            fill(255, 0, 0);
            ellipse(x,y,5,5);
            return;
        } else {
            if(this.nss===undefined){
                fill(255, 0, 0);
                ellipse(x,y,5,5);
            } else {
                line(xs,cy,xl,cy);
                line(cx,ys,cx,yl);
                this.nss.drawHut(p);
                this.nsl.drawHut(p);
                this.nls.drawHut(p);
                this.nll.drawHut(p);
            }
        }
    };

};

This is the key of the Barnes-Hut algorithm. It tells you when to recurse and when not to recurse, and it’s what gives you the series of red masses in the javascript applet above.

The full source code can be found on khanacademy.

1.3 An implementation with dynamics & forces

Javascript on khanacademy is a really poor place to do any high performance computing, but I did write an implementation with 50 particles. You can view the khanacademy source here or click the applet below. (clicking restarts the simulation)

2 Including other forces

The Barnes-Hut method works well for long-range forces, but if we instead want to include short range forces (like a Lennard-Jones force), this would actually be really terrible! I’ve found a good way to do this is making a hash table that stores an integer list of numbers as a key, and a list of particles as values. The integer list is an x/y position (it can be a c++ std::pair<int,int> in two dimensions), and for each particle you only have to check adjacent grid spaces. The Hash table makes sure you can do each lookup in constant time, so the whole thing goes by way faster.

I’m trying to convince you: don’t just plug short-range forces into your gravity code! Do what Part-ND and my code both do, and use a grid! (See for example the 3D collision in Part-ND below.)