In this post, I will show you how to use Mathematica to construct different three dimensional rotation groups, as well as how to generate different mathematical sculptures using the rotation groups.

Download the Mathematica Notebook.

Download the Javascript-style coordinates to 5 digits.

Directory

• Introduction
• The Output
• Creating a group from a generating set
• Finding the Axes of Rotation
• The Whole Code, Mathematica Notebook, and Javascript Coordinates

0 Introduction

I found it very annoying to come up with things like the vertices of an icosahedron, the elements of the icosahedral group, etc. So I wrote a Mathematica script to do it all for me! I used this in my presentation I Heart Group Theory and So Can You.

1 The Output

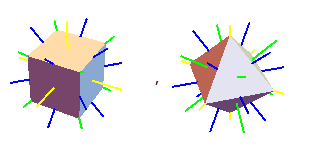
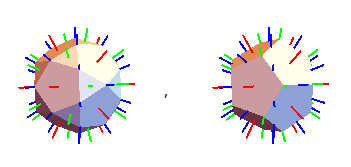
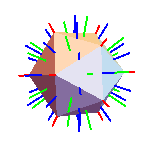
This whole program creates all of the vertices of various polyhedra, all of the group elements of the tetrahedral, octahedral, and icosahedral groups, and all of the rotation axes of said groups. ie, it does basically everything you could care to do for the rotation groups! Below are some examples with their rotational symmetry axes drawn. The axes have a color scheme:

• Axes of 2nd order symmetry (rotation by 180 degrees) are drawn in blue,
• Axes of 3rd order symmetry (rotation by 120 degrees) are drawn in green,
• Axes of 4th order symmetry (rotation by 90 degrees) are drawn in yellow,
• Axes of 5th order symmetry (rotation by 72 degrees) are drawn in red.

tetrahedron and cuboctahedron:

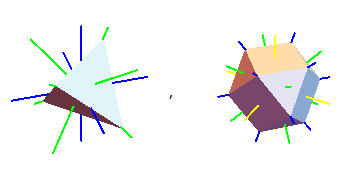
cube and octahedron:

icosadodecahedron and dodecahedron:

icosahedron:

2 Creating a Group from a Generating Set

The rotational icosahedral group contains 60 rotations, that is, 60 three by three matrices. That’s way too many numbers to type out. If you need all sixty matrices, it’s better to generate them programmatically by starting with a generating set.

A list of rotations are said to generate the rotation group $G$ if every element of $G$ can be written as compositions of that list of rotations. For example, you might have a group $G$ consisting of: $G=\{\text{rotate by }0^\circ, \text{rotate by }90^\circ, \text{rotate by }180^\circ, \text{rotate by }270^\circ\}$, but this is generated by the action “rotate by 90 degrees”. You can repeatedly apply this one rotation to get all the other group elements. You write: $G=\langle\text{rotate by }90^\circ\rangle$. It’s a much more compact notation/idea.

We want to start with the generating set, and apply all elements of the generating set in all possible combinations. We want to repeat this over and over until we don’t get any new results.

The function Tuples[list,2] returns all possible pairs from the argument list in all possible combinations. For example:

In[]:= Tuples[{1,2},2]
Out[]:={ {1,1},{1,2},{2,1},{2,2} }

The Mathematica command #1.#2&@@@pairlist applies the first element in each pair to the second element. So, the command:

list2=FullSimplify[#1.#2]&@@@Tuples[list,2]

Combines all rotations inside list, in all possible orders and pairings. Some of the combinations will lead to the same rotation, so we need to remove duplicate matrices. The Mathematica command for this is usually Union[list2], but Mathematica isn’t able to simplify the matrices in the icosahedral group, and it will leave mathematically identical matrices! I solve this by using the option of Union, SameTest. With this I keep the symbolic accuracy of the rotations, but use only numeric accuracy for the comparisons. The whole function – starting with the generating set and creating a list of all possible combinations of elements of the generating set – looks like this:

iterate[g_] := Union[FullSimplify[#1.#2] & @@@ Tuples[g, 2], SameTest -> (Flatten[N[#1 - #2]].Flatten[N[#1 - #2]] < 0.01 &)];

Then, given a generating set “generators”, I can create the whole group by simply using:

group=FixedPoint[iterate, generators]

3 Finding the Axes of Rotation

Given a matrix, how do you find what axis it rotates about, inside Mathematica?

I tried to be clever/efficient about this, but in the end I just plugged each matrix into the Mathematica Eigensystem command, and chose the unique eigenvector with eigenvalue one. Transpose[Eigensystem[r]] gives me a list of the form { {eigenvalue, eigenvector},{eigenvalue, eigenvector},…}. I can select the one with eigenvalue one by using Select[%,#[[1]]==1&], and get only the vector by taking %[[1,2]]. All-in-all:

(* Find the invariant axis of a three dimensional rotation matrix by selecting for the 
 only eigenvector with eigenvalue one. *)
rotAxis[r_] :=  Select[Transpose[Eigensystem[r]], #[[1]] == 1 &][[1, 2]];

What I really wanted to do was find the rotation axes and color them by their order. If they’re rotations by 180 degrees, they’re of order two, since two 180 degree rotations does nothing overall. 120 degree rotation, order three. 90 degree rotation, order four, et cetera. This can be done by successively applying a matrix to itself until I get the identity element:

(* Numerically check if a square matrix is the identity matrix to 
within some accuracy *)
isIdentityMatrix[r_] := (Flatten[N[r - IdentityMatrix[Length[r]]]].Flatten[
N[r - IdentityMatrix[Length[r]]]] < 0.001);

(* Find what integer power you have to raise a matrix to to get the
identity. eg, given integer "m", the command 
getMatrixOrder[RotationMatrix[2Pi/m,{1,0,0}]] will return "m". *)
getMatrixOrder[r_] := Module[{n, mat}, n = 1; mat = r;
   While[n < 100 && Not[isIdentity[mat]],
    mat = N[mat.r];
    n = n + 1;
   ];
   n
  ];

4 The Whole Code, Mathematica Notebook, and Javascript Coordinates

Download the Mathematica Notebook: mathandcode.com/media/pointgroup3D_polyhedra.nb

Download the Javascript style coordinates to 5 digits. (components of the tetrahedral, octahedral, and icosahedral 3D rotation point groups, lists of all their axes of rotation, and lists of the vertices of some polyhedra)

The whole code

(* Numerically check if a square matrix is the identity matrix to \
within some accuracy *)

isIdentityMatrix[
   r_] := (Flatten[N[r - IdentityMatrix[Length[r]]]].Flatten[
      N[r - IdentityMatrix[Length[r]]]] < 0.001);

(* Numerically check if any matrix is the zero matrix to within some \
accuracy *)
isZeroMatrix[r_] := (Flatten[N[r]].Flatten[N[r]] < 0.001);

(* Numerically test and remove duplicate matrices from a list *)

reduce[list_] := Union[list, SameTest -> (isZeroMatrix[#1 - #2] &)];

(* Given a list of square matrices g, this function combines all \
possible pairs of matrices in all possible orders, and numerically \
removes all duplicate matrices *)

iterate[g_] := reduce[FullSimplify[#1.#2] & @@@ Tuples[g, 2]];

(* Given a generating set of matrices, this function creates a group. \
If the generators aren't actually a generating set, 
this code runs forever! *)

makeGroup[generators_] := 
  FixedPoint[iterate, Join[generators, {IdentityMatrix[3]}]];

(* Find what integer power you have to raise a matrix to to get the \
identity. eg,
given integer "m", the command \
getMatrixOrder[RotationMatrix[2Pi/m,{1,0,0}]] will return "m". *)

getMatrixOrder[r_] := Module[{n, mat}, n = 1; mat = r;
   While[n < 100 && Not[isIdentity[mat]],
    mat = N[mat.r];
    n = n + 1;
    ];
   n
   ];

(* Find the invariant axis of a three dimensional rotation matrix by \
selecting for the  only eigenvector with eigenvalue one. *)

rotAxis[r_] := 
  Select[Transpose[Eigensystem[r]], #[[1]] == 1 &][[1, 2]];

(* In finding axes of rotation, we wish to remove all duplicate axes.
An axis is a line passing through the origin, and I choose to represent
it by a unit vector. However, the unit vector {-1,0,0} and {1,0,0} \
both 
represent the same axis -- the line {x,0,0}. We can negate the unit 
vector arbitrarily, and we can use this freedom to ensure that the \
leftmost number 
is positive. This function does just that: negates a 3D vector to \
ensure the 
leftmost component is positive. *)

orderAxis[v_] := If[v[[1]] < 0, -v, If[v[[1]] == 0,
    If[v[[2]] < 0, -v, If[v[[2]] == 0,
      If[v[[3]] < 0, -v, v], v]], v]];

normalize[v_] := Simplify[v/Sqrt[v.v]];

getRotationAxes[group_] := Module[{lists, myfunction},
   (* "lists" is of the form { {order,axis},{order,axis},{order,axis} }
   where "axis" is a vector whose leftmost coordinate is positive, 
   and "order" is an integer between 2 and 5 inclusive. *)
   
   lists = {getMatrixOrder[#], orderAxis[rotAxis[#]]} & /@ group;
   (* Select elements from list with a given order, 
   remove duplicates, and normalize *)
   
   myfunction[n_] := 
    normalize /@ reduce[Select[lists, #[[1]] == n &][[All, 2]]];
   { {2, myfunction[2]} (* all axes of order two *),
    {3, myfunction[3]} (* all axes of order three *),
    {4, myfunction[4]} (* all axes of order four *),
    {5, myfunction[5]} }];

orbit[point_, group_] := reduce[#.point & /@ group];

(* Tetrahedron generators, group elements, and all axes of rotation *)

tetGenerators = {RotationMatrix[2 Pi/3, {1, 0, -1/Sqrt[2]}], 
   RotationMatrix[2 Pi/3, {0, 1, 1/Sqrt[2]}]};
tetG = makeGroup[tetGenerators];
tetaxes = getRotationAxes[tetG];
tetaxes2 = tetaxes[[1, 2]];
tetaxes3 = tetaxes[[2, 2]];

(* Octahedron generators, group elements, and all axes of rotation *)

octGenerators = {RotationMatrix[Pi/2, {1, 0, 0}], 
   RotationMatrix[Pi/2, {0, 1, 0}]};
octG = makeGroup[octGenerators];
octaxes = getRotationAxes[octG];
octaxes2 = octaxes[[1, 2]];
octaxes3 = octaxes[[2, 2]];
octaxes4 = octaxes[[3, 2]];

(* Icosahedron generators, group elements, and all axes of rotation *)

f = (1 + Sqrt[5])/2;
icoGenerators = { { {-1, 0, 0}, {0, -1, 0}, {0, 0, 01} }, { {0, 0, 1}, {1,
      0, 0}, {0, 1, 0} }, 
   1/2 { {1, -f, 1/f}, {f, 1/f, -1}, {1/f, 1, f} } };
icoG = makeGroup[icoGenerators];
icoaxes = getRotationAxes[icoG];
icoaxes2 = icoaxes[[1, 2]];
icoaxes3 = icoaxes[[2, 2]];
icoaxes5 = icoaxes[[4, 2]];

tetV = orbit[tetaxes3[[2]], 
  tetG]; (* tetrahedron vertices *)
cubeoctV = 
 orbit[octaxes2[[2]], octG];(* cuboctahedron vertices *)
cubeV = 
 orbit[octaxes3[[1]], octG]; (* cube vertices *)
octV = 
 orbit[octaxes2[[1]], octG]; (* octahedron vertices *)
icosadodecaV = 
 orbit[icoaxes2[[1]], 
  icoG]; (* icosadodecahedron vertices *)
dodecaV = 
 orbit[icoaxes3[[1]], icoG]; (* dodecahedron vertices *)
icosaV = 
 orbit[icoaxes5[[1]], icoG]; (* icosahedron vertices *)


drawhull[verts_] := 
  Graphics3D[{EdgeForm[], 
    GraphicsComplex[MeshCoordinates@#, MeshCells[#, 2]] &[
     ConvexHullMesh[verts]]}, Boxed -> False];
drawhull /@ {tetV, cubeoctV, cubeV, octV, icosadodecaV, dodecaV, 
  icosaV}


drawhullAxes[verts_, axes_] := 
  Graphics3D[{Thick, 
    Transpose[{ {Blue, Green, Yellow, 
       Red}, (Line[{1.2 #, -1.2 #}] & /@ #) & /@ axes[[All, 2]]}], 
    EdgeForm[], 
    GraphicsComplex[MeshCoordinates@#, MeshCells[#, 2]] &[
     ConvexHullMesh[verts]]}, Boxed -> False];
drawhullAxes @@@ { {tetV, tetaxes}, {cubeoctV, octaxes}, {cubeV, 
   octaxes}, {octV, octaxes}, {icosadodecaV, icoaxes}, {dodecaV, 
   icoaxes}, {icosaV, icoaxes} }