A common exercise in mechanics involves taking some complicated nonlinear system, linearizing it around its equilibrium, and then finding the resonant frequencies of that system. This Mathematica code does that automatically for a mesh of springs.

If you're asking why a mesh of springs would be nonlinear, it's because these springs have a nonzero unstretched length. The energy isn't $U=\frac{1}{2}kr^2$, it's $U=\frac{1}{2}k(r-r_0)^2$, with $r=\sqrt{x^2+y^2}$.

I've seen this in introductory level mechanics, advanced mechanics, and graduate level mechanics, so this is probably worthy of a longer article.

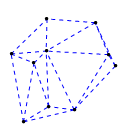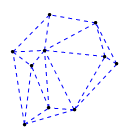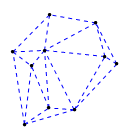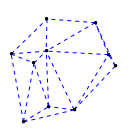
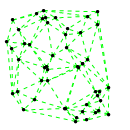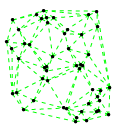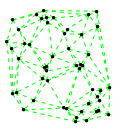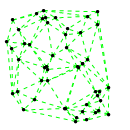
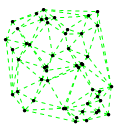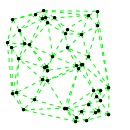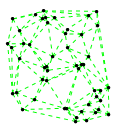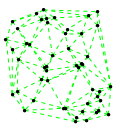
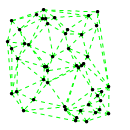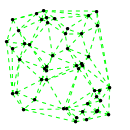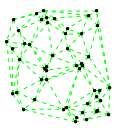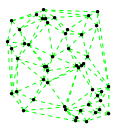
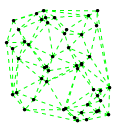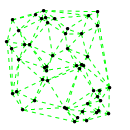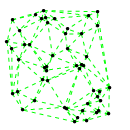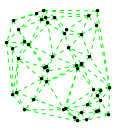
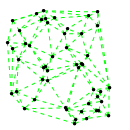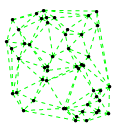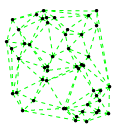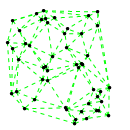
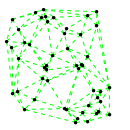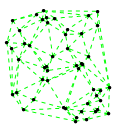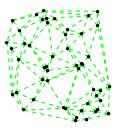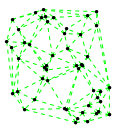
Mathematica source:

<< ComputationalGeometry`
pts=Join[RandomReal[{-1,1},{45,2}]^3-0.4,RandomReal[{-1,1},{45,2}]^3+0.4];
pts=RandomReal[{-1,1},{50,2}];
edges=Union[Union/@Flatten[(Function[y,{#1,y}]/@#2)&@@@DelaunayTriangulation[pts],1]];
springk=1&/@edges;
masses=1&/@pts;
kmat=SparseArray[Join[edges,(Reverse/@edges )]->Join[springk,springk]];
normalized[v_]:=If[v.v>0,v/Sqrt[v.v],v];
indices=Union[Flatten[edges]];
normals=Table[normalized[pts[[i]]-pts[[j]]],{j,1,Length[indices]},{i,1,Length[indices]}];

(* After linearization, you find that, if kmat[i,j] is the spring constant between points 
i and j and "normals" is pts[[i]]-pts[[j]] normalized and {a[i,1],a[i,2]} is the magnitude of the
 small oscillations, the force on a point i due to all the other springs j is: Sum[-kmat[i,j]
  normals[i,j] normals[i,j].({a[i,1],a[i,2]}-{a[j,1],a[j,2]}),{j,1,3}] *) 
system=Chop@ Eigensystem[(SparseArray[Flatten[Table[{ {2i+s-2,2j+l-2}->kmat[[i,j]]
normals[[i,j,l]]normals[[i,j,s]]},{j,1,Length[indices]},{l,1,2},{i,1,Length[indices]},{s,1,2}]]]-
SparseArray[Flatten[Table[{2i+s-2,2i+l-2}->Sum[kmat[[i,j]]normals[[i,j,l]]
normals[[i,j,s]],{j,1,Length[indices]}],{i,1,Length[indices]},{s,1,2},{l,1,2}]]]
)];
system={Sqrt[-#[[1]]],Partition[#[[2]],2]}&/@Transpose[system[[All,;;-4]]];

pt2[n_,t_,i_]:=pts[[n]]+0.1system[[i,2,n]]Cos[system[[i,1]]t];
plotme[t_,i_]:=Graphics[{ Green,Thin,Dashed,Line[{pt2[#1,t,i],pt2[#2,t,i]}&@@@edges],Black,Table[Disk[pt2[j,t,i],0.03],{j,1,Length[pts]}]},PlotRange->{ {-1.1,1.1},{-1.1,1.1}}];

Then call plotme[t,i] for time t and mode i. Make sure 1<=i<=Length[system].